 The topic of infinity comes up occasionally in apologetics arguments, but this is a lot more involved than most people think. After exploring the subject, apologists may want to be more cautious.
The topic of infinity comes up occasionally in apologetics arguments, but this is a lot more involved than most people think. After exploring the subject, apologists may want to be more cautious.
Philosopher and apologist William Lane Craig walks where most laymen fear to tread. Like an experienced actor, he has no difficulty imagining himself in all sorts of stretch roles—as a physicist, as a biologist, or as a mathematician.
Since God couldn’t have created the universe if it has been here forever, Craig argues that an infinitely old universe is impossible. He imagines such a universe and argues that it would take an infinite amount of time to get to now. This gulf of infinitely many moments of time would be impossible to cross, so the idea must be impossible.
But why not arrive at time t = now? We must be somewhere on the timeline, and now is as good a place as any. The imaginary infinite timeline isn’t divided into “Points in time we can get to” and “Points we can’t.” And if going from a beginning in time infinitely far in the past and arriving at now is a problem, then imagine a beginningless timeline. Physicist Vic Stenger, for one, makes the distinction between a universe that began infinitely far in the past and a universe without a beginning
Hoare’s Dictum is relevant here. Infinity-based arguments are successful because they’re complicated and confusing, not because they’re accurate.
One of Craig’s conundrums is this:
Suppose we meet a man who claims to have been counting from eternity and is now finishing: . . ., –3, –2, –1, 0. We could ask, why did he not finish counting yesterday or the day before or the year before? By then an infinite time had already elapsed, so that he should already have finished by then.… In fact, no matter how far back into the past we go, we can never find the man counting at all, for at any point we reach he will have already finished.
Before we study this ill-advised descent into mathematics, let’s first explore the concept of infinity.
Everyone knows that the number of integers {1, 2, 3, …} is infinite. It’s easy to see that if one proposed that the set of integers was finite, with a largest integer n, the number n + 1 would be even larger. This understanding of infinity is an old observation, and Aristotle and other ancients noted it.
But there’s more to the topic than that. I remember being startled in an introductory calculus class at a shape sometimes called Gabriel’s Horn (take the two-dimensional curve 1/x from 1 to ∞ and rotate it around the x-axis to make an infinitely long wine glass). This shape has finite volume but infinite surface area. In other words, you could fill it with paint, but you could never paint it.
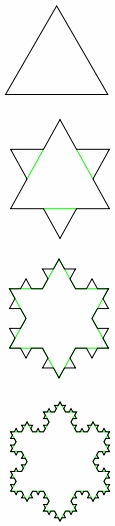
A two-dimensional equivalent is the familiar Koch snowflake. (Start with an equilateral triangle. For every side, erase the middle third and replace it with an outward-facing V with sides the same length as the erased segment. Repeat forever.) At every iteration (see the first few in the drawing above), each line segment becomes 1/3 bigger. Repeat forever, and the perimeter becomes infinitely long. Surprisingly, the area doesn’t become infinite because the entire growing shape could be bounded by a fixed circle. In the 2D equivalent of the Gabriel’s Horn paradox, you could fill in a Koch snowflake with a pencil, but all the pencils in the world couldn’t trace its outline.
Far older than these are any of Zeno’s paradoxes. In one of these, fleet-footed Achilles gives a tortoise a 100-meter head start in a foot race. Achilles is ten times faster, but by the time he reaches the 100-meter mark, the tortoise has gone 10 meters. This isn’t a problem, and he crosses that next 10 meters. But wait a minute—the tortoise has moved again. Every time Achilles crosses the next distance segment, the tortoise has moved ahead. He must cross an infinite series of distances. Will he ever pass the tortoise?
The distance is the infinite sum 100 + 10 + 1 + 1/10 + …. This sum is a little more than 111 meters, which means that Achilles will pass the tortoise and win the race.
Some infinite sums are finite (1 + 1/2 + 1/4 + 1/8 + … = 2).
And some are infinite (1 + 1/2 + 1/3 + 1/4 + … = ∞).
(And this post is getting a bit long. Read Part 2.)
Photo credit: Wikipedia
Related posts:
Related articles:
- “Zeno’s paradoxes,” Wikipedia.
- “Zeno’s Advent Calendar,” xkcd.com.
- “Paradoxes of infinity,” Wikipedia.
- “Is God Actually Infinite?” Reasonable Faith blog.
- Peter Lynds, “On a Finite Universe with no Beginning or End,” Cornell University Library, 2007.
- Mark Vuletic, “Does Big Bang Cosmology Prove the Universe Had a Beginning?” Secular Web, 2000.
- Wes Morriston, “Must the Past Have a Beginning?” Philo, 1999.
- William Lane Craig, “The Existence of God and the Beginning of the Universe,” Truth Journal.

To Bob the atheist,
If the universe is infinite, that is, if it has an infinite amount of particles, is the amount of particles even or odd? However, if the universe is not infinite, yet has no beginning, how can it be anything else than cyclical?
I don’t follow your logic leading to a cyclic universe, but even if I did, I fear that you’re applying common sense thinking to issues at the frontier of science, where common sense is not especially reliable.
I agree that in the area of mathematics, commonsense is not very reliable, but I am making a philosophical objection, which rests on the experience of the physical world. An actual infinite may make sense in mathematics, but it doesn’t in the real world.
I’ve seen some arguments that an actual infinite does make sense (for example, here), though this is beyond my interest.
You referred to mathematics, philosophy, and the real world (which perhaps is physics). My point is that common sense isn’t much help at the frontier of physics. If your common sense is violated when you study the ideas in cosmology, well, get used to it.
“If the universe is infinite, that is, if it has an infinite amount of particles, is the amount of particles even or odd?”
Whether something is even or odd is a property of integers. To ask if “infinity” is even or odd makes no sense because it is not an integer. For a more mundane example, I could ask if pi is even or odd, that question also makes no sense because pi is also not an integer.
The problem is that in the world, there is nothing real but natural numbers. We use mathematical devices to understand how it works, but they do not literally apply to the real world.
Well that is simply incorrect. Natural numbers are only the positive integers. This doesn’t even include negative numbers and fractions. Certainly you don’t mean to say that fractions are only theoretical. Have you ever cut something in half?
I certainly don’t claim that mathematical devices like fractions are useless to understand the world, but they don’t exist literally in the world.
When I cut something in half, I make two things out of one thing, but I never get a “physical” fraction, so to speak. Of course I may say that, for instance, I get half a pie by cutting it, but it’s because I compare one of the current halves with what the pie WAS before it was cut or maybe with my ideal concept of a pie. But such a comparison, involving a fraction, is only possible for a thinking being. in the physical world, such a fraction does not exist as such.
well what if I don’t actually cut the pie, but instead I just want to talk about the left half of it? Certainly now this exists.
But then we are no longer speaking of beings as wholes, we are speaking of the PARTS of beings.
In that sense, yes I may grant that fractions exist in the real world. But there is an arbitrary element, because it is our mind that decides what counts as the part and what counts as the whole. One thing may be both a whole and a part, depending on what we compare it with. On the contrary, natural numbers are fully objective.
But I still maintain that actual infinites don’t exist as such in the real world.
I guess if you are restricting to counting discrete things, then sure, natural numbers are the only relevant numbers. I would argue that other numbers come up in the real world though.
But lets get back to infinities because they are more fun. When you say that infinities don’t exist in the real world, I’m not so sure. You may be right, but I think you may be wrong also. It is conceivable that time is infinite, no matter how far back you go, you can keep going farther back. Granted, we have a beginning of our universe, but perhaps there was something before that which we came from.
If this were the case, then we would be talking about an infinity that exists in reality. Is this really what happened? I don’t know. None of us do really. But I don’t see why it can’t be a possibility.
To Hausdorff,
I don’t claim either that the Big Bang is the time of “divine creation”. I disagree with apologists who try to use the Big Bang for their own ends. No one knows what existed before the time limit set by “Planck’s wall”.
But Big Bang or not, the concept of infinite time seems absurd. Time is logically posterior to change. In speaking of infinite time, we actually speak of an infinite amount of past changes.
But a medieval philosopher, st. Bonaventure, raised an interesting paradox in his attempt to prove that the universe had a beginning. If there was an infinite amount of changes in the past, then some of them are at an finite distance from us, such was yesterday, one year ago, the formation of our planet and on on. But others must be at an infinite temporal distance from us because an infinite amount of changes or events could not fit into a finite temporal line. But in that case, since those events belong to the past, so that they have already elapsed, when did we cross the boundary between changes infinitely remote and changes finitely remote? It makes no sense because any finite amount + 1 unit will still make a finite amount…
So there are only two ways out:
1) Time is linear and the universe had a beginning (and therefore a beginner).
2) Time is cyclical and contains only a finite amount of events which endlessly recur. I cannot imagine a more meaningless world than this one.
Yes, infinite time does sound pretty crazy. But so does finite time.
As for St. Bonaventure, I think he’s struggling with infinty as a number vs. infinity as a concept.
“the concept of infinite time seems absurd”
It does seem fairly crazy. On the other hand, the thought of there not being an infinite amount of time in the past means there must be a beginning. In other words, there is a point where something happens that wasn’t the result of something before it. That seems pretty crazy too. To have the first thing happen just spontaneously with no precursor is hard to imagine. Of the 2 things, an infinite amount of time into the past makes more sense to me. But I do see that both are strange.
“Time is logically posterior to change”
I’m not quite sure I understand what you are saying here. Are you saying we need time first then we can have change? Can you elaborate on this idea?
As to the paradox of Bonaventure, it is the same mistake that was made above. And actually, the key to it is something you said
“an infinite amount of changes or events could not fit into a finite temporal line”
That’s true, for any fixed finite amount of time cannot hold an infinite amount of moments. But for each pair of moments, there is a finite amount of time large enough to encompass both of them.
For example, suppose the finite temporal line we are talking about is between now and 1 year ago. There are a lot of points in time before that. Jan 1 2000 for example, is not in this time period, but it is not an infinite amount of time away, I just need to expand my time frame to about 12 years. If we do that, there are still points in time farther back, but again, they are not an infinite amount of time away, we just need to expand our bubble of time we are looking at.
If there is infinite time, it doesn’t mean that there is a finite bubble big enough to encompass everything. It actually means the opposite, no finite amount will be enough. No matter how big of a finite span of time we consider, there will always be something outside of it. But for each specific point in time, we can find a finite line large enough for it.
It might help to think of time as the number line. Every point in time is some value x on the number line. So if we set ‘right now’ to be zero, then for any moment that happened x minutes ago, we can see it is a finite amount of time ago, it fits into the finite line [-x,0] and is therefore a finite time away. There are no points on the number line and infinite distance from the origin in the same way that there are no moments in time an infinite amount of time in the past.
I hope this makes sense. It would be easier if we were talking face to face, and ideally if I had a chalk board 🙂
Actually, now that I think about it, translating this into natural numbers might make it easier. When you said
“If there was an infinite amount of changes in the past, then some of them are at an finite distance from us…But others must be at an infinite temporal distance from us”
This is equivalent to saying ‘If there are an infinite number of natural numbers, then some of them are finitely large, but others must be infinitely large”
But this is not true, even though no finite interval is large enough to encompass them all, every natural number will fit inside some interval of the form [1,k] and is therefore finite.
(not sure if that helps, but it’s worth a shot I guess)
Oh, one more thing. Since we have talked about fun math stuff this long, I feel I should post a link to vi hart’s videos. If you haven’t seen them before it is totally worth your time.
http://vihart.com/doodling/
Excellent videos! Like the study of Christianity, math is something you can lose yourself in for a lifetime.
Hi Hausdorff,
It’s hard for me to find the right words to translate my hunches. If I had studied mathematics, maybe it would help.
I’m not so sure we can equate a time line with a number line, due to the ontological difference between the physical world and the mathematical realm…
I mean, don’t forget that we are speaking of real PAST events, events that already took place. Suppose we associate each of this past event with a negative number. Then however far we get, we will always get finite time and a beginning. Unless at some point we posit infinitely remote events. Now you say that, however, we can always get further into the past, and that’s the genuine meaning of infinite. But though it’s adequate to speak thusly of a number line, what could it possibly mean for a time line?
You often use expressions such as “for every pair of numbers, there will always be a finite distance. This may be correct in the realm of maths. The problem is to make it clear what we are speaking about when we apply that word “every” to the physical world. What is the range of that “every”? Finite or infinite? Remember that we are speaking of the physical world.
There is also a difference between the past and the future. I can easily conceive an eternal future provided that God exists (that’s what we can heaven and hell). But what it means is that our timespan, though always finite, will endlessly grow. Which by the way is only possible if God, in some sense, is ontologically infinite.
If I may, sometimes it seems to me that the mathematical infinite is less to be seen as some weird “amount” than as a RULE for generating numbers and operations according to our needs. But I may be wrong, because I have little knowledge of maths.
I would think equating a time line with a number line would be a pretty good analogy, I guess the only question would be is time finite (a line segment) finite in the past and infinite in the future (a ray) or infinite both ways (a line). But in any case, a line seems like the best thing we can get.
As to the ontological difference making the analogy break down, there might be something there. I’m not really sure how to explore those ideas though. As far as I can tell, if time does go to infinity in both directions a line should be a good representation, but that could just mean there is some idea I’m missing.
As far as the “for every pair of numbers”, since at the time I was imagining a situation in which there was infinite time, I did mean for it to be any point in the infinite amount of time. So for example, what I was claiming is that for any pair of moments, they both lie in time somewhere, and therefore they are a finite distance apart. What would be the opposite of this? That there are 2 points which are an infinite distance apart. I want to claim that this doesn’t make sense. Why? Because each point of time lies somewhere on this timeline. Since we are saying that time is infinite (we are assuming that just for this argument) then this particular moment can go back as far as it wants. Or in other words, you can never pick a point in time that it will for sure be in front of. But this moment has to lie somewhere in time. Since both moments have to lie somewhere in time, there must be a finite distance between them.
I suppose this all rests on the assumption that time acts like a line (I didn’t realize I was making that assumption until your last comment). I guess I would argue that this assumption is reasonable as I can’t see what else it could be.
Your last comment about infinity being more about a rule rather than being an actual quantity is interesting. It’s sorta correct, depending on the situation. Infinity actually has quite a few different meanings, and I think there is really something to that way of looking at it.
To Hausdorff,
If we looked to the future, I would agree that it makes sense to equate a time line with a number line. But things are different as regards the past because, well, the past ACTUALLY took place, which means that it is for now ACTUALLY some specific amount of elapsed events. I mean, there is a specific amount of years between us and year 2000, or the discovery of America, or the formation of our planet. If we suppose an open future (linear time), then of course there is no specific amount of events between now and some “end” of the world, because there never was such an end. Or let’s imagine an indefinite number of sci-fi writers. One of them imagines the world in 1000 years, another in 5000 years, another in 200 000 years, another in 1 000 000 years, and so on. There is no limit set upon their imagination. This possibility to imagine any future date we want, that’s a genuine infinite.
If however we looked to the past, I say: any finite amount of events we may imagine, however large, would imply a beginning somewhere. Since we are speaking of the past, we are not free to imagine any amount we want: there is one that IS true. While the future is the realm of the possible, the past is the realm of dead facts. There MUST be a time when Columbus made it to America.
A number line is more like the realm of the possible (= the future) than the realm of dead facts (= the past). A more adequate analogy with the past would be a finite set.
For the same reasons, believers must be careful when they speak of an “infinite” God. Some ways of understanding it are nonsensical. I tend to avoid using “infinite” in speaking of God, I prefer to use “perfect” or “supreme” or words like that.
Teapot:
Responding to your last paragraph: how do we know that God is perfect? Does the Bible say so or is this simply implied?
One thing that bugs me is apologists listing all sorts of properties for God that aren’t explicitly stated in the Bible. Even the ones that are in the Bible could, in many cases, be challenged by statements made elsewhere in the Bible. But traits like omnibenevolent or prefect or infinite seem a unsupportable stretch if they’re not explicitly stated in the Bible.
Your thoughts?
To Bob S,
Well, the Bible has Jesus say “be perfect as your celestial Father is perfect”. I don’t know the exact reference, though. The Bible also says that God is holy, which means moral perfection.
OK. Holy doesn’t mean moral perfection to me but rather spiritual goodness–that is, the focus is on the supernatural, while it is on interaction with your fellow man in the case of morality.
But to the bigger issue: do you see Christians extrapolating too much when they list the properties of God? That is, do they make claims about God that have no unambiguous support from the Bible?
To Bob S,
Well, it’s true that theologians like Thomas Aquinas and his followers have lots of things to say about God, and their main support is pagan metaphysics (Aristotle, the Stoics, Plato and Plotinus). But those people really think that they can PROVE their claims (read the beginning of the Summa Theologiae) and as Christians, they hold that reason is compatible with faith.
But I agree that what theologians and philosophers is not always explicitly stated in the Bible. In the case of God’s impassibility, which is supposed to be a philosophical truth, it may even be contrary to the Bible.
Teapot,
What you are saying makes sense only if we start with the assumption that there is a finite amount of time in the past. If there were an infinite amount of time in the past, then the number line backwards would be a good analogy for it.
It appears to me that you are starting by assuming that time is finite, then claiming that an infinite past causes problems. Instead, I think we should imagine an infinite past and see if there is a problem that comes up. If you can’t find a contradiction then such an infinite past is a possibility. As far as I can tell, the only contradiction you have come up with is with the other assumption that you have made, namely that there is a beginning.
If we are considering the idea of an infinite past, it has to be coupled with no starting point. There is no beginning, every point in time has some other point in time preceding it. Yes, it is strange, but it does seem to make sense to me.
To Hausdorff,
Do we at least agree that for there to be an infinite past (whatever that may mean) there needs to be an infinite amount of particles in the universe? Because if their amount is finite, then the amount of their possible states is finite. But if we compare a finite amount of possible states with an infinite time line, we cannot escape the conclusion that there has been cycles.
Let’s take an example. Suppose that the only kind of event that happens in a parallel universe is the rolling of a (fair) die. In that universe, there are only six possible states, depending on what number the die shows at each time. Isn’t it clear that the same numbers will endlessly recur in an infinite time?
At least the odds are for that.
There is definitely something there. Things recurring over and over is certainly a possibility, although I don’t think it is necessary that we wind up in a strictly cyclical situation. Allow me to run with a few ideas for a minute here and see where it takes us.
First, I like your idea of simplifying things by considering rolling a die, I’d like to take this a step further and consider flipping a coin instead. Let’s suppose we are flipping a coin an infinite number of times. You might be inclined to say that at some point, the overall pattern must recur, I say not necessarily. This is easy to see with the following example:
HT HHT HHHT HHHHT…
(I added some spaces to try to make it clear what I’m doing, just after each tails add one more heads than last time before the next tails)
As you can see, this pattern can continue forever without ever repeating in it’s entirety. Furthermore, there will be certain sequences that will show up once, and only one, for example THHT. On the other hand, there are other sequences that will show up an infinite number of times, for example HTH. This must happen, if we look at any specific number of flips (in this case we looked at 3 flips) there is a finite number of possibilities, so at least one of those possibilities must happen an infinite number of times. (in this example, HHT, HTH, THH , HHH happen an infinite number of times, and THT, TTH, HTT, TTT never happen)
I know this sequence is going forward in time, but we can send the same sequence backward in time and we can say a lot of the same things. I could just make the sequence:
…THHHHTHHHTHHTHTHHTHHHTHHHHT…
or something like that.
Ok, now let’s think about the universe. As you suggested, let’s assume that we have an infinite amount of time in the past, and that we have a finite amount of particles, and I want to also assume we have a finite amount of space. Even though there is an unimaginable amount of data (huge numbers of particles, each has position and velocity with respect to each other and who knows what else) this data appears to be finite. And since there is an infinite amount of time, some organization of all of that stuff has to come up over and over again. In fact, as with our simple coin flipping example, some organization of that data has to come up an infinite amount of times.
So if we think about the current organization of the universe, if there was an infinite amount of time in the past, can we say it happened before? It is certainly possible, but what if it corresponds to the THHT from the example? If that is the case, this moment in time has never been before and will never happen again. On the other hand, it could be like HHH and it has happened an infinite number of times before and will happen an infinite number of times in the future.
Sorry for the super long comment. I could go on and on like this (I’m having fun here) but I think I’ll just stop for now and hope I’m making sense to you guys.
Yep, I’m listening!
I don’t have much to add, except to note that it’s refreshing to see a discussion continue politely, as this one has.
Doesn’t always happen …
To Hausdorff,
I’m considering writing a little paper (in French) about my views about how atheism seems to imply eternal recurrence. So I find our dialogue helpful.
Let’s stick to the coin which is flipped, and let it represent a simplified model for our own universe, assuming it is finite.
You say that some combinations will recur an infinite amount of times. Others will recur only once. I have to disagree.
If you assume that the series of H/T had a beginning and stretches infinitely forward, then yes, you would be right. That’s why heaven will not be cyclical, even though it lasts forever.
But we are dealing with something more bizarre: an infinite past.
You say that sequences like THHT will happen only once. True, if the series has a beginning. Wrong, if it has no beginning. If it has no beginning, it has happened an infinite amount of times, and here is why.
Suppose I granted you that THHT happened only once. Let’s say it happened one billion years ago. But since we are dealing with an infinite past, the timespan before one billion years ago is also infinite. But if we hold that THHT has a nonzero probability, then over an infinite timespan, its probability of manifestation becomes one. Which means that it must have happened more than one time, it must have happened before one billion years ago. And whenever it happened, the timespan before that time must be infinite, because it’s a property of the infinite past.
If it were not a property of the infinite past, then the infinite would consist of the sum of finite amounts, which is absurd. Infinite + any finite amount = Infinite, therefore Infinite – any finite amount = Infinite. Is that correct in your view? The second equation, if correct, represents the infinite past.
What I am getting at is that, over an infinite time (without a beginning), any combination of H/T with nonzero probability must have happened an infinite amount of times…
And that’s what I mean by a cyclical time.
This is really good stuff, I’ve been thinking about what you have said, in particular the idea that any event that has a non-zero probability over an infinite amount of time actually has a probability of 1. This certainly sounds correct, but something has been tugging at my brain about it that doesn’t sound quite right. Part of the problem I was having is when we talk about flipping a coin, we are usually thinking of a fair coin, one where each flip has a 50% chance of heads and a 50% chance of tails. On the other hand, my example from before has a very regular function for what we get. That seems like it couldn’t happen. But it is one of the possible results you could get when you flip a coin an infinite number of times. (fun fact: if you list all of the ways that you could flip a coin an infinite number of times, you get a bigger kind of infinity)
I feel like I’m rambling a bit, sorry. Let’s return to my previous example list,
…THHHTHHTHTHHTHHHT…
In my hypothetical, I have perfect knowledge of the flips in the future and in the past, and in this list, THT only happened once. So let’s think about what I have in this situation. I have a single object being flipped an infinite number of time. There are only a finite number of states that object can hold (2 states, H and T). And yet, we have a situation where a particular pattern only happened once.
You might object that this is not a fair coin. I might agree with you (perhaps, perhaps not, a discussion for another time perhaps), but I would say that is beside the point. Because my understanding is that you were making the following claim:
IF there are a finite number of states for a finite number of particles and time goes to negative infinity THEN every possible state has happened an infinite number of times.
There is nothing in there about the probabilities or anything that would lead to the coin being fair. My example satisfies the if part of this proposition but breaks the conclusion.
There is one other thing I want to address in your post. You talked about something making sense in an infinite future but not in an infinite past. I don’t really differentiate the 2 things, and I don’t see why we would need to. If you have a sequence of head and tails that you can see goes into the infinite future and has some property, why can’t you just run that same sequence into the past and get the exact same property in the past?
Oh! I remembered one more thing I wanted to add. You have said 2 things that are very similar although I think one is right and one is not. You mentioned that if time is infinite and the number of particles is finite, then time must be cyclical. I think this is incorrect, and the reason why I think is encapsulated above. But in the most recent post, you said “seems to imply eternal recurrence”. If by this, you mean that there have to be some patterns (at least 1) that recur an infinite number of times, then I do agree. But there doesn’t necessarily have to some point where everything effectively starts all over.
Hi Hausdorff,
I am not sure I correctly understand your latest points well, because my mathematical skills are limited.
If you suppose an infinite series with a starting point, which grows following a law, then it’s perfectly correct to say that some state will happen just a limited number of times.
But the eternity the atheist considers is different, because it is supposed to be open in both directions: no beginning and no end.
Our actual state of affairs (we may describe it as “discussion on Bob’s blog”) is actual, therefore it had a nonzero probability. Which means it already happened an infinite amount of times in an infinite past. Suppose the last time it happened was 1000 billion years ago, in some pre-big bang world. The fact is that, assuming that the past is infinite, there was an infinite timespan BEFORE that last event. Which means that, as the discussion on Bob’s blog has a nonzero probability, it must have happened still before (maybe 2000 billion years ago). And so on ad infinitum.
However, there is a further complication. If I consider people as physical systems, either deterministic or probabilistic, then that view is correct. But if I endow them with free will, things get confused, because a free choice is irreducible to chance. Someone making a choice is essentially different from a random process in nature. In fact, it has nothing to compare it with.
So it means that in a cyclical world, while there would be the same physical stuff and the same laws, there would be unpredictable events due to free agency. In that sense, it is perfectly sensible to hold that, though the past is infinite, some events due to free agency only happened a finite number of times. At least if I am not mistaken. So it is possible to think that in the next cycle, there would be no World War II for example, though the laws of physics would be identical.
You are also skeptical of my claim that the past is not symmetrical with the future. Of course, if you represent time by number series, with 0 as the present, negative integers as past events and positive integers as future events, you will miss what I am trying to say. Did you even have the idea that in another intelligent species, their civilization would measure time starting from the Big Bang, and in that case, there would be an absolute beginning (0) followed by an indefinite series of integers. It makes sense to me. The system is less practical than ours, but it is coherent. Why think that our system is a better model for time?
Let’s posit an infinite series of negative integers. 0, -1, -2, -3, … Actually, we may just as well choose to make it represent the future. It is only by convention that such a series is made to represent the past. It’s not a bad convention, but it breaks down when we are trying to explore the philosophical meaning of time. Infinite series of numbers, by their very nature, are only fit for representing the future.
Another point I would like to make is that in an infinite timespan, the place we put the zero on our time line is completely arbitrary. We may just put it now, or one billion years ago, or in a billion years from now. But since the place of the zero is completely arbitrary, we can hardly say that some patterns are unique.
If I try to stick to the usual convention of using a number line to represent a time, I may make the zero represent the present and say that every new day, the zero shifts one notch forward, so that a new series begins each day, and patterns we thought were unique will recur.
I hope that makes some sense, though you are really pushing me to the limits of my intelligence.
Hi OT,
I have a number of comments to make and I might not get to them all, so if there is something I seem to be skipping over feel free to point it out again.
I think we actually agree on a fair bit of this, it might not seem that way because I have been focusing on points of disagreement. For example, the cyclical universe is something that I think sounds very plausible, and I think is a definite possibility. The idea that there is an infinite amount of time so anything that has any small probability of happening must happen, and in fact must happen an infinite number of times sounds very compelling. It might be right. I’m not quite convinced it has to be though. There are several nagging thoughts that I have which seem to demonstrate counterexamples to this. I’ve tried to explain some of these ideas, but I think those explanations have been confusing at best as I am still working through the ideas myself. Also, while I feel like I have counterexamples to the infinite cycles idea, I am having some trouble punching holes in the idea itself. My gut still says that an infinite cyclical past is a possibility but not a necessity.
As to the 2 directional infinity versus the 1 directional infinity. I’m not convinced that for us it makes much of a difference. Suppose for example that you can prove that an event has happened an infinity number of times in the past, can’t you use the same logic to show that it will also happen an infinity number of times in the future? If I can show that it is possible that this moment will never happen again, couldn’t the same logic be used to show it is possible for that moment to have never happened in the past?
As far as the future being symmetric with the past, I think I was just using that as a quick example of a way something could happen just once. I definitely didn’t mean to imply that I thought that time was symmetric. Another example could be to do one sequence into the future and a different one into the past. Your point about where zero goes I agree with 100%.
(I decided to break this into 2 comments as it was getting long)
Let me try to articulate one of my ideas about why I think it is possible for an event to happen only once even in an infinite amount of time. I want to return to the flipping coins analogy, it is simple enough to understand and I think it illustrates one of the points I keep returning to in my thinking. I want to think about this in the most extreme fashion I can in this setting, so I ask the following:
Q: Is it possible to flip a coin an infinite number of times and get H every time?
You probably want to answer “no” right now, but let me run through some ideas and let’s work up to it.
First, if I flip a coin once what are the odds I get H? 50% or 1/2. Because there are 2 possibilities H or T.
What if I flip a coin twice, what are the odds of getting HH? 1/4. There are 4 possibilities HH,HT,TH,TT. So one out of four chance.
What if I flip a coin 50 times? There are 2^50 possibilities and only one of them is all heads, so my probability of getting all heads is 1/2^50.
In general, if I flip a coin n times, then there are 2^n possibilities and only one of them is all heads, so the probability of getting all heads is 1/2^n.
If n is finite, this little formula works every time. But what happens when we start to talk about flipping an infinite number of times? One thing I might do is take a limit as n goes to infinity, then this probability goes to zero. But if we actually replace n with infinity does the probability actually become zero? Unfortunately, I think the best answer to this question is “sort of”.
Let’s think about this, how many ways are there to flip a coin an infinite number of times? There are an infinite number of ways to do it. So when we ask what the probability is that we get all heads, we are asking what the odds are that we get 1 particular set of rolls out of an infinite number of choices. It might make sense to say that the probability of this is zero. But that is also true for any other set of rolls. Even one that looks fairly random to us, the odds of that particular roll are the same as the one that we recognize as significant (all heads).
When I say it makes sense to call this probability zero, one way to think of this is to try to figure out what the probability is. The probability of something is a number between zero and 1 where 1 means it will happen for sure, and 0 means it can’t happen. For any fraction above zero (call it epsilon), we can say for certain that the odds of rolling all heads out of an infinite number of flips is less than epsilon. We haven’t exactly shown that the probability is zero, but we have shown that it can’t be any number above zero. We can usually think of this a simply being zero, but there are times when we would call this an infinitesimal. The odds of this happening are infinitely small. But it is possible.
I am having trouble telling if this is clear or super confusing. Please feel free to ask for clarification, these ideas are organized fairly well in my head, but I am having trouble putting them into text.
* but I agree that what theologians and philosophers SAY ABOUT GOD
Hi Hausdorff,
I think you may be onto something. It may or may not be possible over an infinite timespan to get only heads or only tails even if the coin is fair.
In fact, one crazy thought is that, as long as the probability of getting heads is not one exactly, it may be possible never to get them over an infinite timespan. The difference between improbable and impossible becomes blurred.
But I don’t know much about probability, so I am not sure how compelling those ideas are. It’s odd to imagine that the odds not to get heads over an infinite timespan are neither zero nor any number above zero. Perhaps one would say that there is no possibility left after that.
You are also right that there are an infinite amount of possible combinations of heads and tails over an infinite time. As long as we don’t limit the span of each cycle. If we say that each cycle lasts only enough time for ten flips, then the possibilities are limited.
(to be continued)
To Hausdorff,
Two other points:
First, I must be clear about what cyclical time means. It means that time oscillates: it goes backward and forward. What is being done will be undone, and what is being undone will be done. So to be accurate, it’s not exactly correct to speak of future or past cycles. It’s just a cognitive bias we have, just as people have lots of trouble understanding the theory of relativity because it runs counter to naive physics hardwired in our brain. It is just hard to use language to explain what a cycle is, because our brains are not “designed” to understand that. We say for instance: the universe will expand, THEN it will shrink, THEN it will bounce back and expand again. But those “then” don’t really make sense in a cyclical time. They are parts of speech, not parts of the idea itself.
One problem is that when we consider cycles, we imagine ourselves as divine observers outside the cycles, and we may imagine ourselves counting them or comparing them. But if EVERYTHING that there is, is within a cyclical world (no external observer) then it makes no sense to think in that way. If there is an external observer, some kind of God, then from his viewpoint, time is linear and the cycles add up. But without that observer, it would be wrong to speak as if time were linear, and there were past and future cycles. We keep speaking like that, because we can’t help ourselves, but we must be careful not to mistake the finger for the thing it points to.
The other point is that in Nietzsche, there is a related argument for eternal recurrence. Nietzsche says: if the universe had a goal, it would already have reached that goal. If time is infinite, it makes sense. What would be a goal that even eternity does not suffice to reach? On the other hand, if we suppose that the universe has no goal, could its evolution be directional? Should it not be cyclical?
Your thoughts?
“It’s odd to imagine that the odds not to get heads over an infinite timespan are neither zero nor any number above zero.”
yeah, it is pretty weird. It is starting to get outside my expertise, but my gut here tells me that the issue is probability. The concepts are all grounded in the finite and when you bring them into the infinite there is some extra care that needs to be taken.
Moving on to your points about cyclical time. I’m not really sure what you mean when you say “It means that time oscillates: it goes backward and forward. What is being done will be undone, and what is being undone will be done.”
What this sounds like to me is that at some point time will stop, and then move backwards. So like, everything that is happening will happen in reverse until we get back to the big bang. Almost like rewinding a VCR. I’m assuming this is not what you mean as it sounds totally bizarre to me.
When you talk about cycles this makes more sense to me. If you will allow me, I will expand on what I think you are saying and we can see if our ideas match up.
For the sake of argument, let’s assume the “start” of a cycle is the big bang. The universe expands for a while, then stops expanding, then starts collapsing in on itself. Eventually, the universe collapses all the way into a singularity only to explode again in the “next” big bang. The “next” cycle has started.
Now, if time is cyclical, and what I have described is a cycle, then the way the universe looks at 1 second after the big bang is exactly the same every time. The way the galaxies form is exactly the same every time. The way the earth forms is exactly the same every time. And the way I am writing this blog comment is exactly the same every time.
One point you have made is that if this is the case, then it doesn’t necessarily make sense to think of this as the current cycle and the one that come after this as “the next one”, they are the same cycle. It’s better to think of time as a circle that has connected to itself or something. There is no reason to think of them as 2 separate events as they really are exactly the same in every way. I’ll agree with this idea. It is actually very similar to something called modular arithmetic (which we are all familiar with even though most people don’t know it, 1 o’clock and 13 o’clock are the same for example).
I actually think this idea of cyclical time is interesting and possibly true. I just don’t see it is a necessity. It’s possible that the universe collapses down and each time the new universe that spawns is different. It’s possible that we will expand forever and eventually reach heat death. It is possible that each black hole in our universe spawns another universe, each one unique. It could just be that time really did start 14.6 billion years ago and this universe is the only one. All of these things seem possible to me.
As far as the last thing, I don’t think “directional” and “cyclical” are opposites. Perhaps the opposite of directional is randomness. If evolution does not have a direction, I might expect there to be an incredible amount of branching, which seems to be what happened.
Hi Hausdorff,
I think you have correctly understood what I mean by cyclical time. It’s hard to explain in words. It’s like if time were like this number series: 1, 2, 3, 2, 1, 2, 3, 2, 1, 2, 3, and so on… Or like hours on a clock, as you suggested.
I certainly don’t suggest that my view of cyclical time implies an oscillating universe (big bangs and big crunches alternatively). It does not exclude it either. In fact, cyclical time is a philosophical hypothesis which science cannot directly test. It’s true that on the current scientific view, the universe is slowly heading toward a heat death. But we are here talking about events which are supposed to take place in billions of years, and it would be a little bold to hold with certainty to such a cosmological hypothesis.
While it’s true that biological evolution is neither cyclical nor directional insofar as it has no goal (I accept standard evolutionary theory), cosmological evolution must be either directional or cyclical. When I say “directional” I just mean that the future is unlike the past. That the future brings novelties. But here is the trick: if the amount of possible states of the universe is limited, due to its finite amount of particles, the future cannot forever be unlike the past, it cannot forever bring unexpected things. At some point, the same things will recur. Maybe not in the same order exactly, but it will still be the same things. There is no other alternative: either the future is unlike the past (linear time: directional evolution as I understand that idea) or the future is like the past (cyclical time). In the latter case, we only speak metaphorically of the future and the past.
Another complication is free will. Free will is different from chance and probabilities, though we sometimes confuse the two things. If there is free will, it’s possible that the cycles become unpredictable at the human level, though the stuff and the laws of the universe will be identical. Because free will defies order and predictability.
You say that it’s possible that the universe will end up in a heat death and stay in that state forever. Now I would like to ask you: why did it not happen YET if it’s true that the universe is eternal?
You have raised some interesting points. It may shake my certainties about cyclical time.
I think we are pretty much on the same page on cyclical time. When you said that things don’t necessarily occur in the same order, I agree with that point and think it is a very important point to make. I’m not sure I really like the name cyclical as it seems to imply to me that things will repeat in exactly the same fashion as before. I’m not what I would call it instead though, recurring, or repeating maybe, although repeating has the same problem. Maybe semi-cyclical or quasi-cyclical? I dunno.
The other thought I had, was that this all only works if we have a bounded number of particles, space and time in each cycle. As we have been saying, if we have a fixed amount of particles and an infinite amount of time, then some arrangement of those particles has to repeat. But this isn’t true if the amount of space grows without bound. In this case, you can have a finite amount of space at every given point in time, and yet with space always expanding, there is more room for the particles to spread out and have different organization. The same arrangement doesn’t have to come up. There is a similar thing if the amount of time you are looking at keeps growing. For example, if we are considering a contracting and expanding universe, the whole thing doesn’t ever have to repeat if the length of time between singularities can be arbitrarily large. I hope this is making some kind of sense, basically, I’m looking for ways that infinities can sneak in even though locally everything is finite. BTW, I thought it worth mentioning that the reasoning you are using is called the pigeonhole principle in mathematics.
As to the question about heat death and why it hasn’t happened yet, that is a really good question. I’m not really sure how to answer it, but I do have a couple of ideas.
1. Perhaps heat death and an infinite past are not compatible. As you have argued, there is the possibility of heat death and an infinite past means it should have happened back them at some point. (I’m not a big fan of this one honestly)
2. It is possible to have an infinite past of “interesting” things happening and at some point it results in heat death. Hard to comprehend but that just the way it is. (Note sure I like this one too much either)
3. Maybe each universe spawns new universes with their black holes. So even if they go to heat death it is not really and end of things. This is a way to have both. The biggest problem I see with this one is each new universe would have fewer particles.
Fun musings, but I don’t think I really have a good answer to that question.
To Hausdorff,
Well, I feel this friendly discussion is approaching its conclusion, because I think we have covered the essentials.
There are a few extra points I would like to make.
You are speaking of a universe growing forever. The problem is that to me, any though of an expanding universe implies a starting point. A state in which the universe was the smallest possible. And a starting point is precisely what is excluded by the idea of an eternal universe. Believers agree the created world will exist forever. But they don’t agree that the world has existed ab aeterno.
If we return to our coin to be flipped, it’s true that the series of H/T could be infinitely complex if we don’t put an end to it. Still, there are only two states which can recur, and each H is identical with the others. As you say, it may not be exactly the definition of a cycle, but it’s closely related to it.
If we take a real-life example, we may count the series of years of war and years of peace since the dawn of civilization, and we would get an unpredictable series. Yet there are only two possible states with a nonzero probability: war and peace.
I’m not sure the idea of an infinite past of interesting events ending in a heat death makes any sense. If heat death happens, then it was a possible state, with a nonzero probability. But over an infinite timespan, it should already have happened, not yesterday, not 10 billion years ago, but an infinite time ago.
My point is that the philosopher is faced with a choice: either divine creation in a finite past, or something like cyclical time, with the same set of events recurring forever, even if their order turns out to be unpredictable.
Yeah, I agree, this conversation is starting to get cyclical =D
Seriously though, I had a really good time talking about these things with you. Looking forward to more interesting conversations in the future.
Thanks. The same for me.